Finding Particular Solution for Diophantine Equation

Diophantine Equation

A Diophantine equation is an equation in which only integer solutions are allowed.

Hilbert's 10th problem asked if an algorithm existed for determining whether an arbitrary Diophantine equation has a solution. Such an algorithm does exist for the solution of first-order Diophantine equations. However, the impossibility of obtaining a general solution was proven by Yuri Matiyasevich in 1970 (Matiyasevich 1970, Davis 1973, Davis and Hersh 1973, Davis 1982, Matiyasevich 1993) by showing that the relation (where is the th Fibonacci number) is Diophantine. More specifically, Matiyasevich showed that there is a polynomial in , , and a number of other variables , , , ... having the property that iff there exist integers , , , ... such that .

Matiyasevich's result filled a crucial gap in previous work by Martin Davis, Hilary Putnam, and Julia Robinson. Subsequent work by Matiyasevich and Robinson proved that even for equations in thirteen variables, no algorithm can exist to determine whether there is a solution. Matiyasevich then improved this result to equations in only nine variables (Jones and Matiyasevich 1982).

Ogilvy and Anderson (1988) give a number of Diophantine equations with known and unknown solutions.

A linear Diophantine equation (in two variables) is an equation of the general form

(1)

where solutions are sought with , , and integers. Such equations can be solved completely, and the first known solution was constructed by Brahmagupta. Consider the equation

(2)

Now use a variation of the Euclidean algorithm, letting and

			(3)
			(4)
			(5)
			(6)

Starting from the bottom gives

so

Continue this procedure all the way back to the top.

Take as an example the equation

(11)

and apply the algorithm above to obtain

(12)

The solution is therefore , .

The above procedure can be simplified by noting that the two leftmost columns are offset by one entry and alternate signs, as they must since

			(13)
			(14)
			(15)

so the coefficients of and are the same and

(16)

Repeating the above example using this information therefore gives

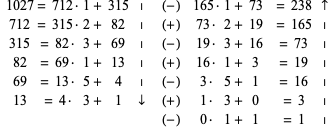(17)

and we recover the above solution.

Call the solutions to

(18)

and . If the signs in front of or are negative, then solve the above equation and take the signs of the solutions from the following table:

equation

In fact, the solution to the equation

(19)

is equivalent to finding the continued fraction for , with and relatively prime (Olds 1963). If there are terms in the fraction, take the th convergent . But

(20)

so one solution is , , with a general solution

with an arbitrary integer. The solution in terms of smallest positive integers is given by choosing an appropriate .

Now consider the general first-order equation of the form

(23)

The greatest common divisor can be divided through yielding

(24)

where , , and . If , then is not an integer and the equation cannot have a solution in integers. A necessary and sufficient condition for the general first-order equation to have solutions in integers is therefore that . If this is the case, then solve

(25)

and multiply the solutions by , since

(26)

D. Wilson has compiled a list of the smallest th powers of positive integers that are the sums of the th powers of distinct smaller positive integers. The first few are 3, 5, 6, 15, 12, 25, 40, ...(OEIS A030052):

			(27)
			(28)
			(29)
			(30)
			(31)
			(32)
			(33)
			(34)
			(35)
			(36)

Wolfram Web Resources

Mathematica » The #1 tool for creating Demonstrations and anything technical.	Wolfram|Alpha » Explore anything with the first computational knowledge engine.	Wolfram Demonstrations Project » Explore thousands of free applications across science, mathematics, engineering, technology, business, art, finance, social sciences, and more.
Computerbasedmath.org » Join the initiative for modernizing math education.	Online Integral Calculator » Solve integrals with Wolfram|Alpha.	Step-by-step Solutions » Walk through homework problems step-by-step from beginning to end. Hints help you try the next step on your own.
Wolfram Problem Generator » Unlimited random practice problems and answers with built-in Step-by-step solutions. Practice online or make a printable study sheet.	Wolfram Education Portal » Collection of teaching and learning tools built by Wolfram education experts: dynamic textbook, lesson plans, widgets, interactive Demonstrations, and more.	Wolfram Language » Knowledge-based programming for everyone.

Finding Particular Solution for Diophantine Equation

Source: https://mathworld.wolfram.com/DiophantineEquation.html

Share :